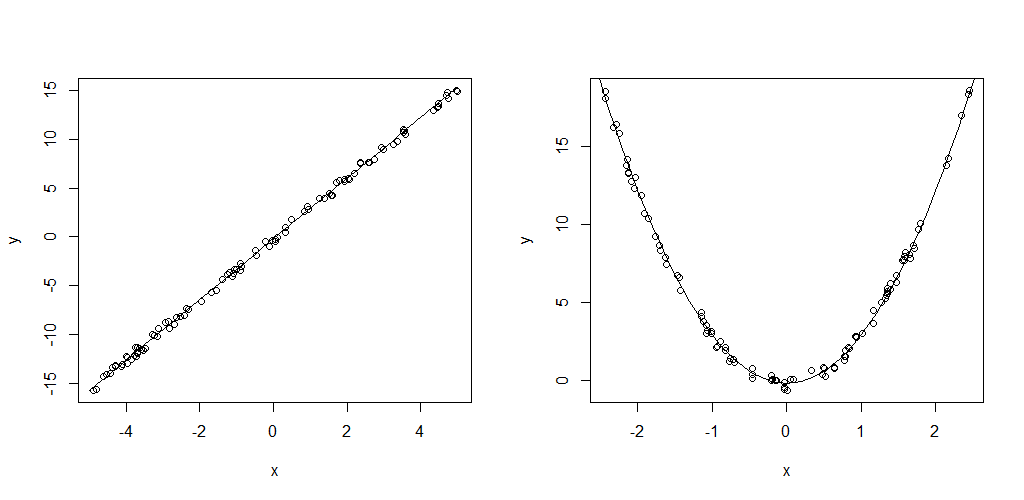
V předešlých příkladech byly řešeny klasifikátory, tedy modely rozhodující o náležitosti záznamu do nějaké ze známých tříd. Oproti tomu metody regrese se snaží o nalezení křivky popisující jeden z atributů. Pomocí této křivky je následně možné odhadnout reálnou hodnotu pro danou kombinaci vstupních atributů. Pouze ve výjimečných případech se stane, že křivka modelu bude procházet datovými body vstupní množiny. Křivka je volena tak, aby se minimalizovala některá z chybových metrik.
U klasifikace se ke srovnávání modelů používá poměr správných odhadů, případně se využije váhovaná confusion matice. U regrese se využívá číselných metrik, které vyjadřují, jak moc se zvolená křivka odlišuje ve známých datových bodech od očekávané hodnoty. Jednou z často používaných obecných metrik je odmocnina ze střední čtvercové chyby (Root Mean Squared Error) (RMSE). Menší hodnota znamená, že křivka lépe modeluje data.
sum((skutečná_hodnota - odhad)^2)
RMSE = sqrt( ─────────────────────────────────── ), kde n = počet datových bodů
n
Druhou ze zajímavých metrik je odmocnina z relativní čtvercové chyby (Root Relative Squared Error) (RRSE). Výsledkem je poměr odhadovaných chyb vůči situaci, kdy by odhadem byla střední hodnota náhodné proměnné (což je ve své podstatě situace ZeroR algoritmu, který u regrese odhaduje vždy střední hodnotu). Hodnota 100% může sloužit jako baseline ke srovnání algoritmů podobně, jako u klasifikátorů byl použit výsledek ZeroR algoritmu.
sum((skutečná_hodnota - odhad)^2)
RRSE = sqrt( ──────────────────────────────────────────── ),
sum((skutečná_hodnota - střední_hodnota)^2)
V tomto cvičení jsou využívány datasety linear.csv a quadratic.csv ve kterých je sto (x,y) měření lineární, resp. kvadratické funkce. Do hodnot y je zanesena náhodná složka (šum), aby nebylo řešení triviální. Funkce mají předpis:
y = (3.1x - 0.2) + (RAND()-0.5) y = (3.1x^2 - 0.2) + (RAND()-0.5)
Dataset s lineární funkcí lze importovat do Weka přes Explorer - Preprocess - Open file - zvolit *csv. Po importu je potřeba ověřit, že se jako target atribut zvolil atribut y (tučně označený popisek sloupce v Edit okně) a že jsou atributy chápány jako numerické. Na tento problém je nejlepší použít lineární regresi (classifiers.functions.LinearRegression), která vypočte koeficienty a, b lineární funkce na základě trénovací množiny. Ve výstupním okně je kromě předpisu funkce modelu (y = 3.087x - 0.255) i údaj o RMSE. Pravým kliknutím na výsledný model v Result list a výběrem Visualize classifier errors lze vykreslit datové body tak, jak je model odhaduje (velikost značky X odpovídá chybě pro daný bod).
| X | Y | XY | X^2 | |
|---|---|---|---|---|
| 60 | 3.1 | 186 | 3600 | |
| 61 | 3.6 | 219.6 | 3721 | |
| 62 | 3.8 | 235.6 | 3844 | |
| 63 | 4.0 | 252 | 3969 | |
| 65 | 4.1 | 266.5 | 4225 | |
| 311 | 18.6 | 1159.7 | 19359 | sum() |
Pro ukázku uvádím výpočet lineární regrese na datasetu v tabulce 2. Vzorce pro výpočet lineární regrese jsou:
y = ax + b
n * sum(XY) - sum(X)sum(Y) 5 * 1159.7 - 311 * 18 13.9
a = ────────────────────────────── = ───────────────────────── = ────── = 0.18784
n * sum(X^2) - (sum(X))^2 5 * 19359 - 311^2 74
sum(Y) - a * sum(X) 18.6 - 0.18784 * 311
b = ───────────────────── = ────────────────────── = -7.964
n 5
y = 0.188x - 7.964
Na druhý z datasetů (kvadratická funkce) již lineární regrese kvůli svému omezení na polynom 1. řádu nebude stačit. RRSE lineární regrese je dokonce >100%, tedy horší než baseline. K vymodelování datasetu je potřeba algoritmus, který dokáže pracovat s polynomy vyššího stupně. K tomu lze použít classifiers.functions.SMOreg. Se SMO (optimalizátor pro support vector machines) bylo pracováno již u klasifikátoru Titanic datasetu, toto je algoritmus podobného principu vhodný pro regresi. U klasifikace SVM rozdělovalo prostor tak, aby podél dělící čáry bylo co nejširší pásmo bez jakéhokoliv datového bodu. V případě regrese se SVM snaží najít funkci nejlépe pasující na trénovací dataset. V parametrech modelu je nutné zvolit kernel, což je charakteristika křivky. V tomto případě je ideální PolyKernel (polynom) a v jeho parametrech nastavit exponent 2 (polynom 2. řádu). U reálných dat bývá problém odhadnout stupeň polynomu, v takových případech je potřeba vyzkoušet několik variant v Experimenteru, nebo použít plugin pro optimalizační činnosti.
Při práci s datasetem Titaniku jsme narazili na velké množství chybějících hodnot ve sloupci age. Jelikož jde o číselný atribut, můžeme se pokusit regresí vytvořit model, kterým bychom mohli chybějící hodnoty odhadnout.
Použijeme arff soubor s odstraněnými sloupci se jmény, lístky a kajutami. Atribut age označíme jako target. Dataset nyní rozdělíme na trénovací množinu (záznamy s vyplněnou hodnotou) a výpočetní množinu (záznamy s chybějící hodntou). K odstranění záznamů s chybějícím věkem lze použít filters.unsupervised.instance.RemoveWithValues. V konfiguraci je nutné nastavit do parametru attributeIndex pořadí atributu age a zvolit matchMissingValues = true. Po aplikování filtru v datasetu zbyde 714 záznamů. Dataset uložte pod jiným názvem a vraťte filtrovací operaci tlačítkem Undo. Druhý dataset lze vytvořit přes editaci, seřazení podle sloupce age, označení řádek s vyplněnou hodnotou a volbou Delete ALL selected instances. Dataset opět uložte pod jiným názvem.
Protože nedokážeme předem odhadnout, jaký model by na problém pasoval nejlépe, zkusíme v Experimenteru ověřit několik variant. V novém experimentu zvolte, že se jedná o regresi, vyberte dataset s odstraněnými neúplnými záznamy a do algoritmů přidejte ZeroR jako baseline, LinearRegression, SMOreg s normalizací dat a s PolyKernel o stupních {1,2,3}, IBk pro {3,7,11,21} nejbližších hodnot, REPTree a RandomForest.
Žádný ze zvolených algoritmů se neukázal jako statisticky lepší než ostatní (viz tabulka 3), ale všechny jsou lepší než ZeroR. Použijeme lineární regresi, která se z testovaných jeví jako nejjednodušší. Očekávaná chyba tohoto modelu na neznámých datech je 12.54 ± 1.07 let. Ve weka exploreru otevřeme soubor s úplnými záznamy a na záložce Classify vybereme lineární regresi. V Test options měníme na supplied test set a vybereme soubor s chybějícími údaji o věku. V more options nastavíme výstup předpovědí do PlainText. Výsledný vzorec lineárního modelu je:
age = -4.1115 * sibsp +
-0.9536 * parch +
-2.0577 * embarked=C +
-7.7428 * pclass +
6.6971 * survived_binarized=0 +
45.9351
Všimněte si, že tento model má určité nedostatky. Konkrétně jde o predikování záporné hodnoty věku, která vyplývá ze struktury rovnice (záporné váhy).
| Dataset | (1) | (2) | (3) | (4) | (5) | (6) | (7) | (8) | (9) | (10) | (11) | |||||||||||||||||||||
| 'titanic | 12.54 | ± 1.07 | 12.65 | ± 1.13 | 12.60 | ± 1.17 | 12.92 | ± 2.15 | 12.77 | ± 1.19 | 12.62 | ± 1.24 | 12.79 | ± 1.29 | 12.75 | ± 1.20 | 12.47 | ± 1.24 | 12.47 | ± 1.13 | 14.49 | ± 1.09 | v | |||||||||
| Key | |
| (1) | functions.LinearRegression '-S 0 -R 1.0E-8 -num-decimal-places 4' -3364580862046573747 |
| (2) | functions.SMOreg '-C 1.0 -N 0 -I \"functions.supportVector.RegSMOImproved -T 0.001 -V -P 1.0E-12 -L 0.001 -W 1\" -K \"functions.supportVector.PolyKernel -E 1.0 -C 250007\"' -7149606251113102827 |
| (3) | functions.SMOreg '-C 1.0 -N 0 -I \"functions.supportVector.RegSMOImproved -T 0.001 -V -P 1.0E-12 -L 0.001 -W 1\" -K \"functions.supportVector.PolyKernel -E 2.0 -C 250007\"' -7149606251113102827 |
| (4) | functions.SMOreg '-C 1.0 -N 0 -I \"functions.supportVector.RegSMOImproved -T 0.001 -V -P 1.0E-12 -L 0.001 -W 1\" -K \"functions.supportVector.PolyKernel -E 3.0 -C 250007\"' -7149606251113102827 |
| (5) | lazy.IBk '-K 3 -W 0 -A \"weka.core.neighboursearch.LinearNNSearch -A \\\"weka.core.EuclideanDistance -R first-last\\\"\"' -3080186098777067172 |
| (6) | lazy.IBk '-K 7 -W 0 -A \"weka.core.neighboursearch.LinearNNSearch -A \\\"weka.core.EuclideanDistance -R first-last\\\"\"' -3080186098777067172 |
| (7) | lazy.IBk '-K 11 -W 0 -A \"weka.core.neighboursearch.LinearNNSearch -A \\\"weka.core.EuclideanDistance -R first-last\\\"\"' -3080186098777067172 |
| (8) | lazy.IBk '-K 21 -W 0 -A \"weka.core.neighboursearch.LinearNNSearch -A \\\"weka.core.EuclideanDistance -R first-last\\\"\"' -3080186098777067172 |
| (9) | trees.REPTree '-M 2 -V 0.001 -N 3 -S 1 -L -1 -I 0.0' -9216785998198681299 |
| (10) | trees.RandomForest '-P 100 -I 100 -num-slots 1 -K 0 -M 1.0 -V 0.001 -S 1' 1116839470751428698 |
| (11) | rules.ZeroR '' 48055541465867954 |