Rank correlation

In statistics, a rank correlation is any of several statistics that measure the relationship between rankings of different ordinal variables or different rankings of the same variable, where a "ranking" is the assignment of the labels "first", "second", "third", etc. to different observations of a particular variable. A rank correlation coefficient measures the degree of similarity between two rankings, and can be used to assess the significance of the relation between them.

Context

If, for example, one variable is the identity of a college basketball program and another variable is the identity of a college football program, one could test for a relationship between the poll rankings of the two types of program: do colleges with a higher-ranked basketball program tend to have a higher-ranked football program? A rank correlation coefficient can measure that relationship, and the measure of significance of the rank correlation coefficient can show whether the measured relationship is small enough to likely be a coincidence.

If there is only one variable, the identity of a college football program, but it is subject to two different poll rankings (say, one by coaches and one by sportswriters), then the similarity of the two different polls' rankings can be measured with a rank correlation coefficient.

Correlation coefficients

Some of the more popular rank correlation statistics include

1. Spearman's ρ
2. Kendall's τ
3. Goodman and Kruskal's Îł

An increasing rank correlation coefficient implies increasing agreement between rankings. The coefficient is inside the interval [−1, 1] and assumes the value:

• 1 if the agreement between the two rankings is perfect; the two rankings are the same.
• 0 if the rankings are completely independent.
• −1 if the disagreement between the two rankings is perfect; one ranking is the reverse of the other.

Following Diaconis (1988), a ranking can be seen as a permutation of a set of objects. Thus we can look at observed rankings as data obtained when the sample space is (identified with) a symmetric group. We can then introduce a metric, making the symmetric group into a metric space. Different metrics will correspond to different rank correlations.

General correlation coefficient

Kendall (1944) showed that his $\tau$ (tau) and Spearman's $\rho$ (rho) are particular cases of a general correlation coefficient.

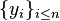Suppose we have a set of $n$ objects, which are being considered in relation to two properties, represented by $x$ and $y$, forming the sets of values $\{x_i\}_{i\le n}$ and $\{y_i\}_{i\le n}$. To any pair of individuals, say the 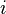$i$-th and the $j$-th we assign a $x$-score, denoted by $a_{ij}$, and a $y$-score, denoted by $b_{ij}$. The only requirement made to this functions is anti-symmetry, so $a_{ij}=-a_{ji}$ and $b_{ij}=-b_{ji}$. Then the generalised correlation coefficient $\Gamma$ is defined by

$\Gamma = \frac{\sum_{i,j = 1}^n a_{ij}b_{ij}}{\sqrt{\sum_{i,j = 1}^n a_{ij}^2 \sum_{i,j = 1}^n b_{ij}^2}}$

Kendall's $\tau$ as a particular case

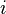If $r_i$ is the rank of the $i$-member according to the $x$-quality, we can define

$a_{ij} = \sgn(r_j-r_i)$

and similarly for $b$. The sum $\sum a_{ij}b_{ij}$ is twice the amount of concordant pairs minus the discordant pkairs (see Kendall tau rank correlation coefficient). The sum $\sum a_{ij}^2$ is just the number of terms $a_{ij}$, equal to $n(n-1)$, and so for $\sum b_{ij}^2$. It follows that $\Gamma$ is equal to the Kendall's $\tau$ coefficient.

Spearman's $\rho$ as a particular case

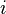If $r_i$, $s_i$ are the ranks of the $i$-member according to the $x$ and the $y$-quality respectively, we can simply define

$a_{ij} = r_j-r_i$

$b_{ij} = s_j-s_i$

The sums $\sum a_{ij}^2$ and $\sum b_{ij}^2$ are equal, since both $r_i$ and $s_i$ range from $1$ to $n$. Then we have:

$\Gamma = \frac{\sum (r_j-r_i)(s_j-s_i)}{\sum(r_j-r_i)^2}$

now

$\sum_{i,j = 1}^n (r_j-r_i)(s_j-s_i)= \sum_{i=1}^n \sum_{j=1}^n r_is_i + \sum_{i=1}^n \sum_{j=1}^n r_js_j - \sum_{i=1}^n \sum_{j=1}^n (r_is_j+r_js_i)$

$=2n\sum_{i=1}^n r_is_i - 2 \sum_{i=1}^n r_i \sum_{j=1}^n s_j$

$=2n\sum_{i=1}^n r_is_i - \frac12 n^2(n+1)^2$

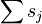since $\sum r_i$ and $\sum s_j$ are both equal to the sum of the first $n$ natural numbers, namely $\frac12n(n+1)$.

We also have

$S = \sum_{i=1}^n (r_i-s_i)^2 = 2 \sum r_i^2 - 2\sum r_is_i$

and hence

$\sum(r_j-r_i)(s_j-s_i) = 2n\sum r_i^2 - \frac12n^2(n+1)^2 - nS$

$\sum r_i^2$ being the sum of squares of the first $n$ naturals equals $\frac16n(n+1)(2n+1)$. Thus, the last equation reduces to

$\sum(r_j-r_i)(s_j-s_i) = \frac16n^2(n^2-1) - nS$

Further

$\sum(r_j-r_i)^2 = 2n\sum r_i^2-2\sum r_ir_j$

$= 2n\sum r_i^2-2(\sum r_i)^2 = \frac16n^2(n^2-1)$

and thus, substituting into the original formula these results we get

$\Gamma_R = 1-\frac{6\sum d_i^2}{n^3-n}$

where $d_i = x_i - y_i,$ is the difference between ranks.

which is exactly the Spearman's rank correlation coefficient $\rho$.

References

• Everitt, B. S. (2002), The Cambridge Dictionary of Statistics, Cambridge: Cambridge University Press, ISBN 0-521-81099-X 
• Diaconis, P. (1988), Group Representations in Probability and Statistics, Lecture Notes-Monograph Series, Hayward, CA: Institute of Mathematical Statistics, ISBN 0-940600-14-5 
• Kendall, M. G. (1970), Rank Correlation Methods, London: Griffin, ISBN 0-85264-199-0