Johnson SU distribution
From Wikipedia, the free encyclopedia
|
|
This article needs attention from an expert in Statistics. The specific problem is: completion to reasonable standard for probability distributions. (November 2012) |
| Parameters |  (real) (real) |
|---|---|
| Support | 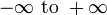 |
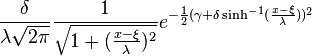 |
|
| CDF | 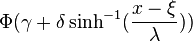 |
| Mean |  |
| Variance |  |
The Johnson  distribution is a four-parameter family of probability distributions first investigated by N. L. Johnson in 1949.[1] Johnson proposed it as a transformation of the normal distribution:[2]
distribution is a four-parameter family of probability distributions first investigated by N. L. Johnson in 1949.[1] Johnson proposed it as a transformation of the normal distribution:[2]
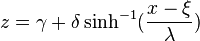
Where 
Generation of random variables[edit]
Let U be a random variable that is uniformly distributed on the unit interval [0, 1]. Johnson  random variables can be generated from U as follows:
random variables can be generated from U as follows:
where Φ is the cumulative distribution function of the normal distribution.
References[edit]
- Jump up ^ Johnson, N. L. (1949) Systems of frequency curves generated by methods of translation. Biometrika 36: 149–176 JSTOR 2332539
- Jump up ^ N.L. Johnson, Table to facilitate fitting SU frequency curves, Biometrika 1949
Additional reading[edit]
- I. D. Hill, R. Hill and R. L. Holder, Algorithm AS 99: Fitting Johnson Curves by Moments, Journal of the Royal Statistical Society. Series C (Applied Statistics), Vol. 25, No. 2 (1976)
- Jones, M. C.; Pewsey, A. (2009). "Sinh-arcsinh distributions". Biometrika 96 (4): 761. doi:10.1093/biomet/asp053. ( Preprint)
|
||
