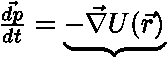
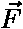
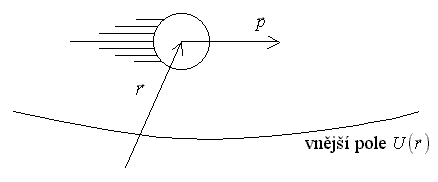
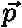 :
:
|
|
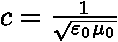
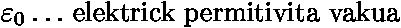
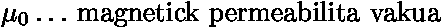
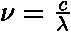
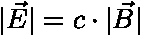
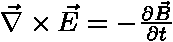
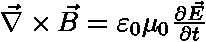
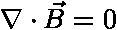
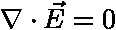
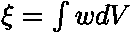 ,
,
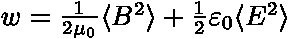 ,
,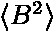 a
a 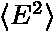 vyjadřuje střední hodnoty, pro které platí:
vyjadřuje střední hodnoty, pro které platí: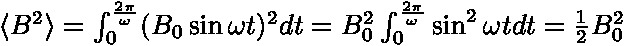
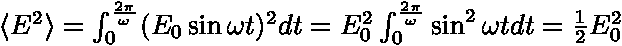
| w | ... | objemová hustota energie |
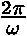
|
... | délka jedné periody |
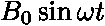
|
... | okamžitá hodnota indukce v čase t |
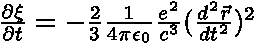
|
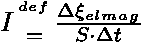
|
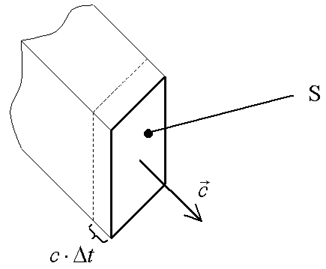
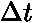 projde plochou S elektromagnetická energie obsažené v kvádru o objemu
projde plochou S elektromagnetická energie obsažené v kvádru o objemu 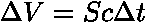 .
.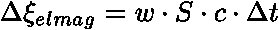
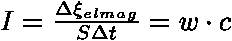
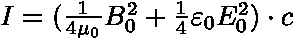
|
|
- Stefan-Boltzmanův zákon |
| T | ... | absolutní teplota tělesa |
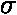
|
... | univerzální konstanta 5,67 * 10-8 [W m-2 K-4] (Stefan-Boltzmanova konstanta) |
| e | ... | emisivita povrchu tělesa (podíl vlastního záření tělesa k celkovému záření, které obsahuje záření odražené z vnějšku) |
| e=0 | ... | těleso vůbec nevyzařuje vlastní záření, veškeré jeho záření pochází z odrazu vnějšího záření ("absolutně bílé těleso", totální reflektor) |
| e=1 | ... | veškeré záření pochází ze samotného tělesa, vnější záření je zcela absorbováno (totální absorbér, "absolutně černé těleso") |
| materiál | e |
|---|---|
| leštěná ocel | 0,07 |
| zoxidovaná mosaz | 0,60 |
| nátěr | 0,97 |
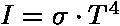
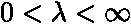 (
(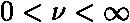 ).
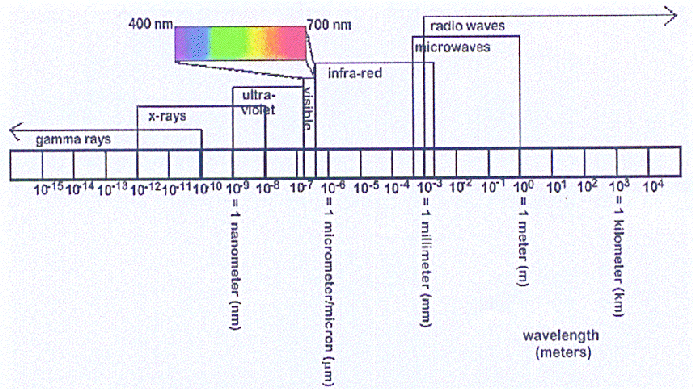
).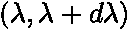 , resp. frekvencemi v intervalu
, resp. frekvencemi v intervalu 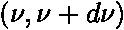 .
.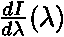 nebo
nebo 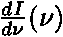
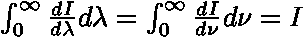
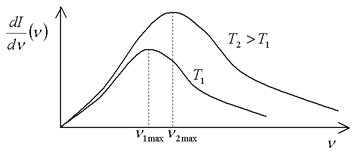
Empiricky se zjistilo, že obecně platí:
|
- Wienův posunovací zákon |
Pro grafické znázornění funkcí 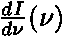 zavádíme termín vyzařovací křivky.
zavádíme termín vyzařovací křivky.
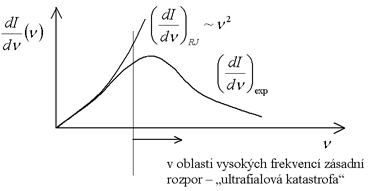
Ukážeme nyní vyzařovací křivky při různých teplotách pro konkrétní tělesa:
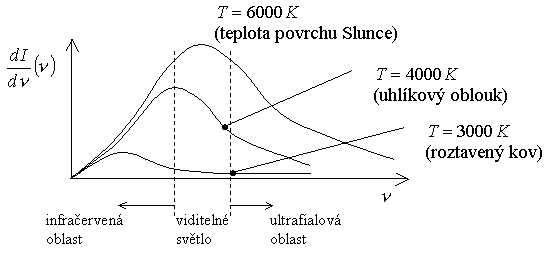
Problém je v tom, že žádnou kombinací zákonitostí klasické fyziky se výše uvedený tvar vyzařovacích křivek nepodařilo vysvětlit.
Klasická fyzika uměla říci toto:
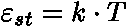 , k=1,381 * 10-23 [J K-1] - Boltzmanova konstanta (poznatek z termodynamiky)
, k=1,381 * 10-23 [J K-1] - Boltzmanova konstanta (poznatek z termodynamiky)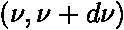 je:
je:
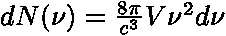
|
| c | ... | rychlost světla |
| V | ... | objem absolutně černého tělesa |
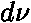
|
... | šířka intervalu záření |
Součin 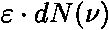 představuje střední energii v intervalu frekvencí
představuje střední energii v intervalu frekvencí 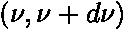 , kterou za jednotku času vyzáří harmonické oscilátory rozmístěné na jednotce plochy povrchu absolutně černého tělesa. Jedná se o intenzitu záření:
, kterou za jednotku času vyzáří harmonické oscilátory rozmístěné na jednotce plochy povrchu absolutně černého tělesa. Jedná se o intenzitu záření:
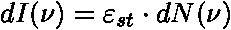
|
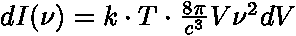
|
- Rayleight-Jeansův vyzařovací zákon (RJ-zákon) |
Další problém upozorňující na nedostatečnost klasické fyziky je fotoelektrický jev.
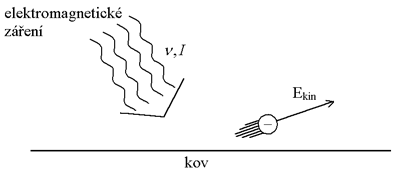
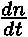 - počet elektronů vylétnuvších z kovu za jednotku času
- počet elektronů vylétnuvších z kovu za jednotku času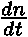
| Co se očekávalo | Co se měřilo |
|---|---|
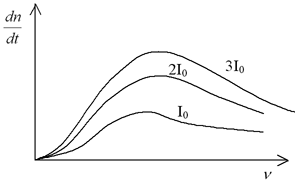
|
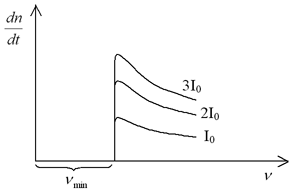 platí: 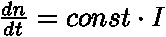
také platí: 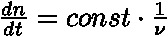 ,
, 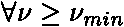
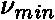 je materiálová konstanta nezávislá na vlastnostech záření
je materiálová konstanta nezávislá na vlastnostech záření
|
| Teorie | Experiment |
|---|---|

Energie vlny se předává elektronu velkou rychlostí, přeto to nějakou dobu trvá:
|
|

|
| Teorie | Experiment | ||
|---|---|---|---|
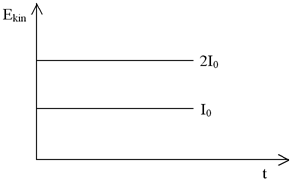
|
|||
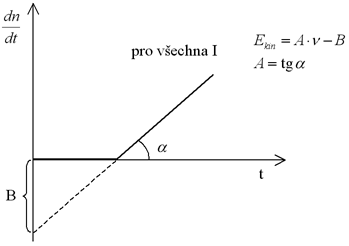
Pro různé materiály:
|
| Očekávané výsledky (dle Maxwellovy teorie) | Experiment |
|---|---|
|
|
|
|
|
Experimentem vydedukován vztah pro 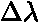 :
: ![$\Delta\lambda=2,426\cdot10^{-12}\cdot(1-\cos\Phi) [m]$](vzorec68.gif) (energie závisí na směru).
(energie závisí na směru).
Potvrzení fotoefektu, navíc ta 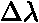 .
.

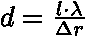 (pro
(pro 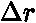 malé)
malé)

Objekt, o kterém předpokládali, že je klasická Newtonovská částice (hmotná) se chová jako elektromagnetické vlnění - podléhá interferenci.
Zkoumali i souvislost interferenčního obrázku a hybnosti: znali d, změřili 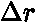 a l ==> vypočetli
a l ==> vypočetli 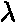 :
:
 (1)
(1)
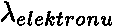 srovnávali s
srovnávali s 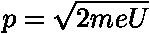

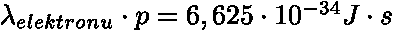
Je zde asi nějaká hlubší souvislost - vystupuje zde stejná konstanta.
Podle zákonitostí klasické elektrodynamiky (Maxwell) by libovolný atom v důsledku vysílaného záření měl zaniknout za dobu kratší než 10-10.
Ve skutečnosti jsou atomy stabilní a vyzařují energii neustále, aniž ji tam cokoli dodává.
Atomy září poněkud jinak než absolutně černé těleso.
|
spojité spektrální záření (spousta čarových, přístroji neměřitelných) |
čarové spektrum záření - toto záření je neměnnou charakteristikou daného prvku |