Petr Girg, KMA, ZČU v Plzni
Stránka vznikla za podpory projektu Matematika pro inženýry 21. století - inovace výuky matematiky na technických školách v nových podmínkách rychle se vyvíjející informační a technické společnosti,
Reg. číslo: CZ.1.07/2.2.00/07.0332
Stránka používá MathJax pro zobrazení matematického textu a Wolfram CDF Player.Cílem této stránky je vysvětlit, že počítačem generovaný graf funkce se může od skutečného grafu funkce velmi lišit. Nejprve si připomeňme definici grafu reálné funkce.
Definice. Grafem funkce \(f\) rozumíme množinu všech uspořádaných dvojic \((x, f(x))\in\mathbb{R}^2\), kde \(x \in D(f)\subset\mathbb{R}\), tj. \[ G_f \stackrel{\mathrm{def}}{=} \left\{ (x,y)\in\mathbb{R}^2\colon x \in D(f)\subset\mathbb{R} \wedge y = f(x) \right\}\,. \]
Z této definice je vidět, že graf reálné funkce není obecně konečná množina (graf reálné funkce je nekonečná množina, kdykoliv je \(D(f)\) nekonečná množina). Tím, že číslicový počítač má k dispozici konečnou paměť a konečný počet výpočetních cyklů, nelze obecně graf spojité funkce v počítači ani vytvořit a ani v paměti uchovat. Graf generovaný počítačem je tedy pouhou aproximací grafu funkce stanovenou na základě (přibližně) vypočtených hodnot konečného počtu bodů grafu funkce. Počet a volba těchto bodů má pak zásadní vliv na dobu potřebnou k výpočtu na jedné straně a věrnost počítačem vygenerovaného grafu na druhé straně. V praxi je třeba najít vhodný kompromis mezi dobou potřebnou k výpočtu (ovlivněno hlavně počtem bodů) a kvalitou grafického výstupu.
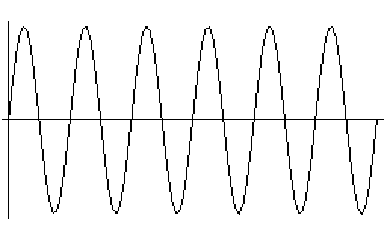
V dobách, kdy nejlepší grafické výstupy na monitoru počítače vypadaly jako na následujícím obrázku, nebylo o aproximatívním charakteru výstupu z počítače pochyb.
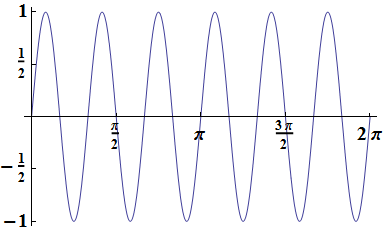
Dnes, kdy výstup vypadá o mnoho lépe jako na sledujícím obrázku, a počítač s internetem je primárním zdrojem informací, často vzniká mylný dojem, že graf funkce je to, co nakreslí počítač.
Nejprve si však musíme vysvětlit, co je to počítačový graf funkce. V první řadě je třeba si uvědomit, že počítačem vygenerovaný graf funkce je závislý na grafickém výstupním zařízení, na kterém má být vykreslen. Pro jednoduchost budeme uvažovat zjednodušený model černobílého LCD displeje. Budeme uvažovat zařízení, které je vytvořeno ze základních obrazových prvků pixelů. Pixel je obdelníková ploška, která může nabývat \(k\in\mathbb{N}\) diskrétních úrovní šedi (od bílé až po černou). U nejjednodušších zařízení je \(k=2\) (bílá a černá). Pixely jsou uspořádány do obdélníkové matice \(m\times n\), takzvané rozlišení monitoru (v současné době typicky \(1280×800\) nebo \(1600\times 1200\), dříve např. legendární počítač ZX-spectrum podporoval rozlišení obrazu \(256\times 192\)). Toto zařízení budeme nazývat idealizovaný LCD displej.
Reálná zařízení typu LCD displej jsou o něco komplikovanější, ale princip je stejný.
Možné stavy našeho idealizovaného LCD displeje lze tedy popsat maticí \(m\times n\), jejíž prvky \(a_{ij}\) nabývají \(k\in\mathbb{N}, k\geq 2\) hodnot \(0, \dots, k-1\). Idealizovaný LCD displej může tedy nabývat celkem \(k^{m\times n}\) stavů.
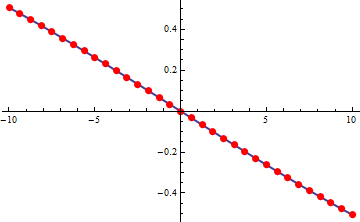
Počítačový graf funkce je jedním ze stavů idealizovaného LCD displeje. Následující aplikace ukazuje, že i počítačový graf úsečky se většinou velmi liší od naší geometrické představy.
Návod. Aplikace simuluje idealizovaný LCD displej o rozlišení \(50\times 50\), \(100\times 100\) a \(150\times 150\). Zobrazuje se stav monitoru reprezentující úsečku s počátečním bodem \((-\cos\phi, -\sin\phi)\) a koncovým bodem \((\cos\phi, \sin\phi)\), bod \((0,0)\) je uprostřed displeje. Při volbě zaškrtnuté volbě Antialiasing se uvažuje idealizovaný LCD displej s \(256\) úrovni šedi, jinak se uvažuje idealizovaný LCD displej se dvěma hodnotami pixelů bílá a černá. Pro převod úsečky na stav displeje se používají algoritmy typu Wu (zaškrtnutá volba Antialiasing) a Bresenham.
Návod. Aplikace opět simuluje idealizovaný LCD displej o rozlišení \(50\times 50\), \(100\times 100\) a \(150\times 150\). Tentokrát se zobrazuje stav monitoru reprezentující systém posunutých rovnoběžných úseček. Dvě sousední úsečky jsou posunuty o vzdálennost \(d = 0.01, 0.02, \dots, 0.1\). Úsečky jsou určeny počátečním bodem \[\bigl(-\cos\phi + (a d - 1) \sin\phi, -\sin\phi - (a d - 1) \cos\phi\bigr)\] a koncovým bodem \[\bigl(\cos \phi + (a d - 1)\sin\phi, \sin\phi - (a d - 1) \cos\phi\bigr)\,,\] kde \(a = 0, 1, \dots, 2/d\). Při volbě zaškrtnuté volbě Antialiasing se uvažuje idealizovaný LCD displej s \(256\) úrovni šedi, jinak se uvažuje idealizovaný LCD displej se dvěma hodnotami pixelů bílá a černá. Vlevo pod ovládacími prvky se zobrazuje systém těchto úseček v rozlišení, které máte nastavené na vašem skutečném hw displeji.
Algoritmy pro převod úsečky na stav displeje (nebo jeho části) jsou dnes implementovány ve standartních grafických knihovnách případně jsou podporovány přímo hardwarem. Proto při vykreslování grafu funkce reálné proměnné je výhodné nejprve nahradit graf této funkce systémem úseček. Již v tomto kroku může dojít k výrazným odchylkám, jak záhy uvidíte. Převod grafu funkce na stav displeje pak probíhá v následujících krocích:
1. Aproximace grafu funkce systémem úseček.
2. Převod úseček na stav displeje.
Upozornění. Při nevhodné volbě parametrů se aproximace grafu funkce může velmi lišit od grafu funkce. Jako příklad uveďme \(f(x)=1/x\) s definičním oborem \(\mathbb{R}\setminus\{0\}\). Pro volbu \(N = 20, x_{min} = -9.99, x_{max} = 10\) dostaneme tuto aproximaci:
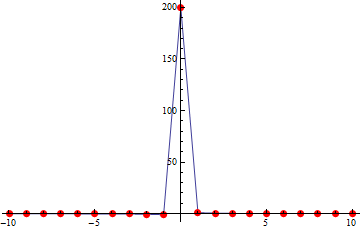
Všimněte si, že nebyl vzat vzorek v bodě \(0\) a tak tento algoritmus nemohl detekovat případnou nespojitost v bodě \(0\). Uvedený obrázek se také bohužel někdy objevuje v písemkách.
Jako další příklady uveďme \(f(x)=\sin 10 x\) s definičním oborem \(\mathbb{R}\). Pro volbu \(N = 32, x_{min} = -10, x_{max} = 10\) dostaneme tuto aproximaci:

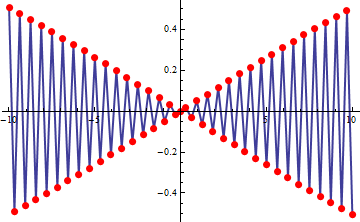
V následující aplikaci si můžete vyzkoušet vliv \(N, x_{min}, x_{max}\) na ``vizuální'' kvalitu aproximace grafů funkcí \(1/x\) a \(\sin 10 x\).
Problém správného vzorkování oscilujících funkcí si vysvětlíme později.
V případě spojité funkce, čím více máme vzorků, tím je aproximace grafu funkce lomenou čarou lepší.
Výpočty v CDF aplikacích, které obsahuje i tato stránka, jsou prováděny jádrem sw Mathematica. Tento software se vždy snaží vytvořit co nejhladší graf adaptivním zjemňováním, tj. přidáváním dalších bodů tam, kde se lomená čára aproximující graf příliš ohýbá [Wagon, Mathematica in Action]. Toto zjemňování probíhá rekurzivně. U nehladkých funkcí by toto mohlo vést k nekonečné rekurzi. Proto je jedním z parametrů algoritmu maximální vnoření rekurze. Dále počáteční vzorkování v sw Mathematica není úplně ekvidistantní, ale od ekvidistantního se málo liší. To dává lepší vstup pro následné adaptivní zjemnění u periodických funkcí, které se často vyskytují v praktických aplikacích (viz problém s ekvidistatním vzorkováním funkce \(\sin 10 x\) výše).
Důvod je ten, že funkce \(-\ln(x)\) na okolí bodu \(x=0\) velmi rychle roste a tento růst nelze na
počítači zachytit. Stačí si uvědomit, že pro daný krok dělení \(h>0\) je
hodnota v prvním bodě následujícím za bodem \(0\) rovna \(-\ln(h)\)
(funkce \(-\ln(x)\) není definována pro \(x=0\)).
V následující aplikaci je ukázáno, jak se mění hodnota prvního vzorku
funkce \(-\ln(x)\) v závislosti na jemnosti vzorkování. Jak jsme si již vysvětlili výše,
sw Mathematica nepoužívá přesně ekvidistantní vzorkování. Proto v tabulce je uveden jak
vzorek následující po \(0\) při ekvidistantním vzorkování, tak i vzorek volený příkazem
Plot následující po \(0\).
V následující aplikaci si můžete zvolit hodnotu \(k\geq 0\), kterou by jste chtěli mít v grafu funkce \(-\ln(x)\). Aplikace vypočte, jaký byl třeba krok vzorkování a minimální počet vzorků na intervalu \([0,1]\). Dále vypočte paměť potřebnou k uchování tohoto počtu vzorků (\(1024\) Bytů = \(1\) KB, \(2^{20}\) Bytů = \(1\) MB, \(2^{30}\) Bytů = \(1\) GB, \(2^{40}\) Bytů = \(1\) TB, \(2^{50}\) Bytů = \(1\) PB, \(2^{60}\) Bytů = \(1\) EB). Budete překvapeni, jak rychle nároky na paměť porostou.
Podobný problém nastává i pro funkci \(\mathop{\mathrm{arctanh}}(x)\) s definičním oborem \((-1,1)\) a oborem hodnot \(\mathbb{R}\). V blízkosti bodů \(-1, 1\) se nedostaneme nad hodnotu \(15\) (a pod hodnotu \(-15\)) ani pro \(100\,000\) vzorků.