Konstrukce rozpoznávacích konečných automatů
Vytvořte přechodové grafy konečných automatů, které rozpoznávají řetězce jistých vlastností nad abecedou {a, b}.
Řetězec obsahuje sudý počet znaků "a".
Při řešení máme dvě možnosti: považovat 0 za sudé číslo:
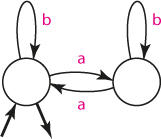
nebo uvažovat pouze přirozená čísla, mezi něž nula nepatří; nejméně tedy akceptujeme dva znaky "a":
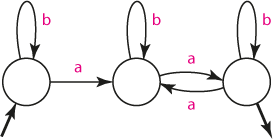
Konstrukce automatů je snadná: na "sudosti" počtu znaků "a" se může podílet pouze znak "a" na vstupu. Proto bude automat přecházet mezi stavy jen znakem "a". Stavy pak vyjadřují, zda automat načetl sudý, lichý, případně nulový počet znaků "a". Znak "b" nemá na sledovanou vlastnost řetězce vliv, proto automat na jeho přítomnost ve vstupu nereaguje, resp. zůstává ve stejném stavu.
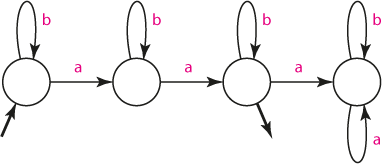
Řetězec obsahuje právě dva znaky "a"
Při konstrukci napřed sestavíme stavy, které postupně znamenají "žádný znak a nebyl nalezen", "byl nalezen jeden znak a", "byly nalezeny dva znaky a". Poslední z nich je stavem akceptačním. Pak připojíme další stav, do něhož se automat dostane načtením třetího znaku a; z něj už se pak nedostane (absorpční stav).
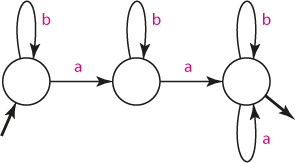
Řetězec obsahuje nejméně dva znaky "a"
Při konstrukci opět využijeme absorpční stav, který bude současně stavem akceptačním:
Řetězec začíná sekvencí "abb-"
Napřed sestrojíme sekvenci stavů, která akceptuje řetězec "abb". Poté připojíme dva absorpční stavy: jeden akceptační, do něhož se automat dostane po načtení "abb", druhý chybový, do něhož se automat dostane v ostatních případech.
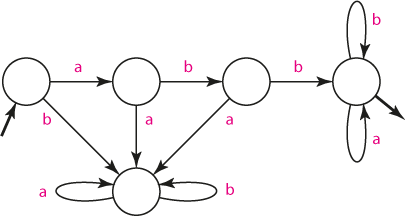
Řetězec obsahuje sekvenci "abba"
Nyní je situace poněkud obtížnější, ale jednoduchým postupem se dá automat rovnž snadno sestavit. Nejprve vytvoříme standardní sekvenci stavů, která odpovídá situacím "načtený vstup končí na a", "končí na ab", končí na "abb", končí na "abba". V posledním stavu zřejmě řetězec obsahuje sekvenci "abba", a proto z něj můžeme udělat absorpční akceptační stav. V ostatních stavech musíme uvažovat způsobem, který si ukážeme na stavu "-ab".
Je-li automat ve stavu "-ab" a na vstupu se objevví "b", končí vstup sekvencí "abb". Jelikož máme pro tuto situaci připravený stav "-abb", může do něj automat přejít. Pokud se ale na vstupu objeví "a", končí vstup sekvencí "aba", což je pro nás mírně nezajímavá situace. Pozornější analýzou zjistíme, že koncová sekvence "aba" znamená, že na konci řetězce se rovněž vyskytují sekvence "ba", respektive "a". Právě poslední jmenovaná ale odpovídá stavu, který vede k rozpoznání řetězce, a proto do něj automat může přejít; říkáme, že řetězec "a" je perspektivním prefixem řetězce "abba".
Tak můžeme sestavit následující tabulku, kde podtržení znamená jednak "část začátku sekvence abba", jednak stav, do něhož automat přechází:
| Stav | |||||
|---|---|---|---|---|---|
| - | -a | -ab | -abb | ||
| Vstup | a | a | aa | aba | abba |
| b | b | ab | abb | abbb | |
Nyní bez potíží nakreslíme přechodový graf:
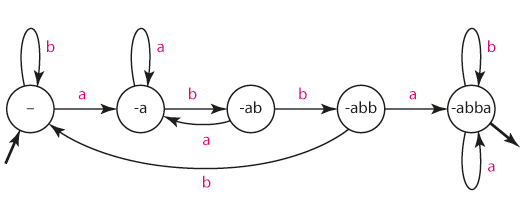
Řetězec nezačínající "bba", obsahující "babb" a nekončící na "aa"
Tento příklad záměrně ukazuje složenou, poměrně komplikovanou podmínku, kterou na řetězec klademe. Ke konstrukci automatu můžeme přistoupit buď systematicky, nebo obdobně jako v minulých případech - postupným rozvíjením jednoduchého automatu. Systematický přístup ukážeme zachvíli; zkusme nejprve automat sestavit "ručně".
Při ručním postupu můžeme uvažovat následovně. Začneme sekvencí stavů, která bude zjišťovat, zda automat začíná sekvencí "bba". Pokud začíná, pak je zřejmé, že řetězec nesmí být akceptován, protože nás zajímají řetězce, které nezačínají sekvencí "bba". Na konci této sekvence proto umístíme absorpční "chybový" stav. Pokud řetězec ze sekvence "bba" uteče, víme, že řetězec na "bba" nezačíná a můžeme se starat o další podmínky.
Dále sestavíme stavy a přechody, které odpovídají rozpoznání podřetězce "babb", a to stejným způsobem, jako v předchozím příkladu. Na rozdíl od něj ale do stavů "-", "-b", "-ba", "-bab", "-babb" můžeme přejít z některého ze stavů, které analyzují začátek řetězce.
Pokud má řetězec splňovat všechny tři podmínky, musí se zjevně napřed rozhodnout, že obsahuje podřetězec "babb", a až naposled rozhodnout, zda končí znaky "aa". Proto můžeme detekci podoby konce řetězce připojit až za stav "babb-".
Tak získáme konečnou podobu automatu. Horní řada stavů odpovídá detekci "bba" na začátku, prostřední řada detekci podřetězce "babb", spodní řada detekci "aa" na konci vstupu. Nezapomeneme označit akceptační stavy v souladu s podmínkou, že řetězec nesmí končit na "aa".
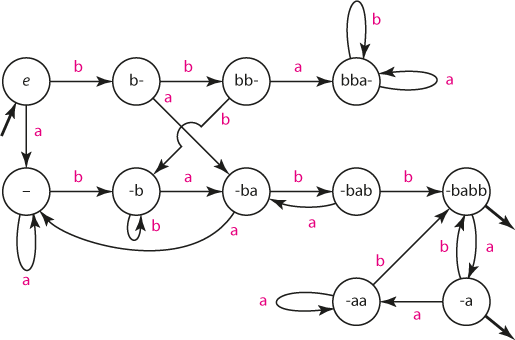
Řetězec obsahující "ba" a neobsahující "bbb"
K sestavení automatu můžeme přistoupit systematicky. Na rozdíl od "ručního" přístupu použitého v předchozím příkladu vede obvykle systematický přístup k větším automatům, výhodou ale je mechanický postup, který může snadno zastat počítač. Tím se dostáváme k podstatné výhodné vlastnosti konečných automatů: velmi často je lze konstruovat, optimalizovat či spojovat prostřednictvím počítačového programu, který se nesplete a který dokáže zvládnout automaty o stovkách tisíc stavů.
Jako ukázku takového algoritmu si ukážeme propojení dvou jednoduchých automatů do jednoho.
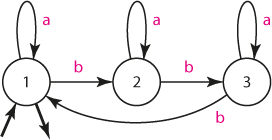
Se zkušenostmi, které máme, můžeme snadno sestavit automat, který zjistí, zda řetězec obsahuje sekvenci "ba"; všem takovým řetězcům budeme říkat jazyk L1.
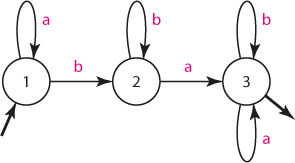
Automat detekující slova obsahující sekvenci "ba"
Formálně zapíšeme definici automatu A1:
- množina stavů Q1 = {1, 2, 3},
- vstupní abeceda Σ = {a, b},
- přechodová funkce δ1 podle grafu výše,
- startovací stav q10 = 1,
- množina koncových stavů F1 = {3}.
Obdobně sestavíme automat A2 akceptující slova jazyka L2, tj. slova neobsahující "bbb":
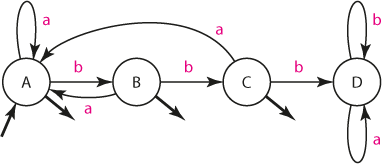
Automat detekující slova neobsahující sekvenci "bbb"
Formálně zapíšeme definici automatu A2:
- množina stavů Q2 = {A, B, C, D},
- vstupní abeceda Σ = {a, b},
- přechodová funkce δ2 podle grafu výše,
- startovací stav q20 = A,
- množina koncových stavů F2 = {A, B, C}.
Nyní vytvoříme automat A akceptující slova jazyka L = L1 ∩ L2, tj. průnik jazyků L1 a L2. Takový automat pomyslně obsahuje oba základní automaty A1 a A2. Jelikož každý z nich se může teoreticky nacházet v libovolném svém stavu, určíme množinu stavů automatu A jako kartézský součin Q1 × Q2:
- množina stavů Q = Q1 × Q2 = {A1, A2, A3, B1, B2, B3, ..., D3}.
Na počátku rozpoznávání by měly být oba základní automaty v počátečním stavu, čili
- startovací stav q0 = A1.
Přechodovou funkci určíme mechanicky: je-li například automat A ve stavu A1 a na vstupu je "b", měl by automat A1 přejít do stavu 2 a automat A2 do stavu B; proto přejde automat A do stavu B2. Stejně sestavíme přechodovou funkci pro ostatní stavy:
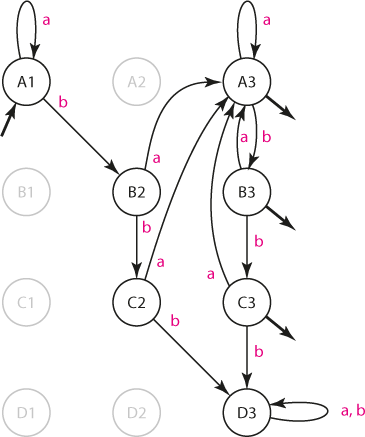
Automat detekující slova obsahující "ba" a neobsahující "bbb".
Stavy označené šedě jsou teoreticky možné, ale prakticky nedosažitelné
Budeme-li stavy automatu A psát ve formě uspořádané dvojice <q1, q2>, kde q1 ∈ Q1, q2 ∈ Q2, potom můžeme formálně přechodovou funkci δ zapsat prostřednictvím funkcí δ1 a δ2: automat A reaguje na vstup x ∈ Σ podle funkce δ
- δ(<qi, qj>, x) = < δ1(qi, x), δ2(qj, x) >.
Stejně tak můžeme formálně zapsat množinu koncových stavů F: pokud chceme, aby automat A akceptoval průnik jazyků L1, L2, potom se musí automat A1 nacházet v některém ze stavů F1 a současně se musí automat A2 nacházet v některém ze stavů F2, tj.
- F = { <qi, qj> | qi ∈ F1 ∧ qj ∈ F2 }
Sjednocení jazyků
Stejným systematickým postupem můžeme vytvořit automat A, který akceptuje slova jazyka L = L1 ∪L2, kde jazyky L1 a L2 jsou rozpoznávány automaty A1 a A2. Neformálně řečeno můžeme vytovřit automat rozpoznávající slova, která by rozpoznal automat A1 nebo automat A2.
Jediným rozdílem oproti předchozímu postupu bude odlišná formulace koncových stavů - místo logického "a" použijeme logické "nebo":
- F = { <qi, qj> | qi ∈ F1 ∨ qj ∈ F2 }
Coby příklad můžeme sestavit automat akceptující sjednocení jazyků L1 a L2, kde
- L1 = { w | w ∈ {a, b}*, w obsahuje podřetězec "abb" a současně nekončí "aa"},
- L2 = { w | w ∈ {a, b}*, počet znaků "b" je dělitelný 3}
(Pozn.: zápis w ∈ {a, b}* označuje všechny řetězce, které lze sestavit ze znaků "a", "b")
Nejprve sestavíme automaty A1 a A2:
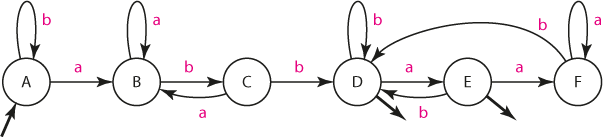
Automat A1
Automat A2
Rutinně sestavíme složený automat:
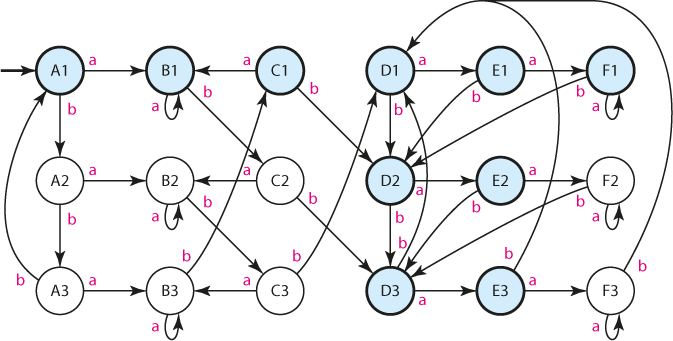
Hotový automat A. Modře zvýrazněné stavy jsou stavy koncovými; výstupní šipky už by obrázek příliš zamotaly
Musíme uznat, že hotový automat není příliš přehledný a jeho přechodový graf se konstruuje poměrně nepohodlně. Zápis přechodové funkce tabulkou je ale triviální. V prvním kroku doplníme, jak by na vstup reagoval automat A1. Všimněme si, že řádky jsou v tabulce řazeny tak, aby byla "písmena" (čili stavy automatu A1) pohromadě. Díky tomu bude v každé "sekci" reakce automatu stejná.
| stav | vstup "a" | vstup "b" |
|---|---|---|
| A1 | B | A |
| A2 | B | A |
| A3 | B | A |
| B1 | B | C |
| B2 | B | C |
| B3 | B | C |
| C1 | B | D |
| C2 | B | D |
| C3 | B | D |
| D1 | E | D |
| D2 | E | D |
| D3 | E | D |
| E1 | F | D |
| E2 | F | D |
| E3 | F | D |
| F1 | F | D |
| F2 | F | D |
| F3 | F | D |
Řádky tabulky si přetřídíme, abychom viděli pohromadě stavy automatu A2, a doplníme jeho reakci:
| stav | vstup "a" | vstup "b" |
|---|---|---|
| A1 | B1 | A2 |
| B1 | B1 | C2 |
| C1 | B1 | D2 |
| D1 | E1 | D2 |
| E1 | F1 | D2 |
| F1 | F1 | D2 |
| A2 | B2 | A3 |
| B2 | B2 | C3 |
| C2 | B2 | D3 |
| D2 | E2 | D3 |
| E2 | F2 | D3 |
| F2 | F2 | D3 |
| A3 | B3 | A1 |
| B3 | B3 | C1 |
| C3 | B3 | D1 |
| D3 | E3 | D1 |
| E3 | F3 | D1 |
| F3 | F3 | D1 |
Nakonec označíme vstupní a výstupní stavy: podle automatu A1 to mají být všechny stavy "D?", "E?", podle automatu A2 to mají být všechny stavy "?1". V případě sjednocení jazyků označíme jako výstupní ty stavy, kde platí alespoň jedna podmínka.
| stav | vstup "a" | vstup "b" | in/out |
|---|---|---|---|
| A1 | B1 | A2 | io |
| B1 | B1 | C2 | o |
| C1 | B1 | D2 | o |
| D1 | E1 | D2 | o |
| E1 | F1 | D2 | o |
| F1 | F1 | D2 | o |
| A2 | B2 | A3 | |
| B2 | B2 | C3 | |
| C2 | B2 | D3 | |
| D2 | E2 | D3 | o |
| E2 | F2 | D3 | o |
| F2 | F2 | D3 | |
| A3 | B3 | A1 | |
| B3 | B3 | C1 | |
| C3 | B3 | D1 | |
| D3 | E3 | D1 | o |
| E3 | F3 | D1 | o |
| F3 | F3 | D1 |
A je to. Poučení je nasnadě: při reprezentaci přechodové funkce (grafem, tabulkou, stromem) využíváme vždy takovou reprezentaci, která je v daný okamžik nejvýhodnější.