KIV / TI - Teoretická informatika
Cvičení 4 - gramatiky

Gramatiky

Základní operace s abecedami

Jsou dány abecedy A = {0, 1, 2}, B = {a, b}. Určete následující množiny:

Přepisovací pravidla

Gramatika G je dána množinou terminálních symbolů T = {a, b, c, 0, 1}, množinou neterminálních symbolů N = {S} a sedmi přepisovacími pravidly

S --> a |  b |  c | Sa | Sc | S0 | S1
     (1)  (2)  (3)  (4)  (5)  (6)  (7)

Jde tedy o levou lineární gramatiku (G3L). Napište odvození následujících řetězců:

Poznámky:

Pro přehlednost znovu uveďme pravidla gramatiky:

S --> a |  b |  c | Sa | Sc | S0 | S1
     (1)  (2)  (3)  (4)  (5)  (6)  (7)

Generování čísel

Napište gramatiku, která bude generovat řetězce představující sudá nezáporná čísla bez znaménka.

Při řešení se odrazíme od faktu, že sudé čílo musí končit číslicí 0, 2, 4, 6 nebo 8. Pokud nám nezáleží na typu gramatiky, který vytvoříme, můžeme obvykle snadno využít gramatiku typu 2 (bezkontextovou):

S --> AB                         (1)
A --> AB | AC | e                (2a-2c)
B --> 0 | 2 | 4 | 6 | 8          (3a-3e)
C --> 1 | 3 | 5 | 7 | 9          (4a-4e)

Pravidla 3a až 3e (pro symbol B) generují číslice, které se mohou vyskytnout na konci sudého čísla. Pravidla 4a až 4e generují ostatní číslice.

Pravidlo 1 tedy říká, že na konci čísla musí stát jen vhodná číslice (symbol B) a před ním může stát libovolný řetězec (A).

Pravidla 2a až 2c (pro symbol A) levorekurzivním způsobem určují, že symbol A se má přepsat na libovolně dlouhý řetězec složený ze symbolů B nebo C, což pokrývá všechny možné číslice.

Příklad vygenerování řetězce 64:

S --> AB           (1)
  --> A4           (3c)
  --> AB4          (2a)
  --> A64          (3d)
  --> 64           (2c)

Alternativně bychom mohli tutéž gramatiku zapsat následujícím způsobem. Je mírně logičtější, protože jasně odděluje "zvláštní číslice" (pravidla pro symbol Z) a "libovolné číslice" (pravidla pro symbol L), ale za cenu duplikování některých pravidel.

S --> RZ                                       (1)
R --> RL | e                                   (2a, 2b)
Z --> 0 | 2 | 4 | 6 | 8                        (3a-3e)
L --> 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9    (4a-4j)

Jiný způsob řešení vyžaduje, abychom napřed sestrojili nedeterministický konečný automat akceptující sudá celá čísla. To uděláme snadno:

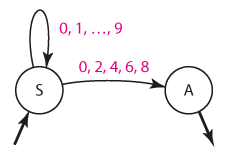
Nyní již rutinně převedeme automat na pravorekurzivní gramatiku:

S --> 0S | 1S | 2S | 3S | 4S | 5S | 6S | 7S | 8S | 9S         (1a-1j)
      0A | 2A | 4A | 6A | 8A                                  (2a-2e)
A --> e

Při převodu využíváme jednoduchých pravidel:

Podotkněme, že ke každému konečnému automatu umíme zapsat ekvivalentní gramatiku. Naopak, ke každé pravorekurzivní regulární gramatice dokážeme sestavit ekvivalentní konečný automat. Ale pozor - k obecné gramatice nemusí existovat ekvivalentní konečný automat!

Napište gramatiku, která bude generovat řetězce představující sudá nezáporná čísla bez znaménka a bez nevýznamových nul na začátku.

Nezáleží-li nám na typu gramatiky, můžeme zavést neterminální symbol K pro "koncovou sudou číslici", symbol L pro libovolnou číslici a symbol N pro nenulovou číslici. Gramatika se startovacím symbolem S je pak:

S --> K | NRK                                   (1a, 1b)
R --> e | LR                                    (2a, 2b)
K --> 0 | 2 | 4 | 6 | 8                         (3a-3e)
L --> 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9     (4a-4j)
N --> 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9         (5a-5i)

Pravidla pro symbol S říkají, že číslo je buď jednociferné (1a), nebo má na začátku nenulovou číslici následovanou řetězcem libovolných číslic a končí správnou koncovou číslicí (1b). Pravidla pro symbol R definují libovolně dlouhý řetězec neterminálních symbolů L čili libovolných číslic.

Alternativně můžeme sestrojit konečný automat a gramatiku odvodit z něj.

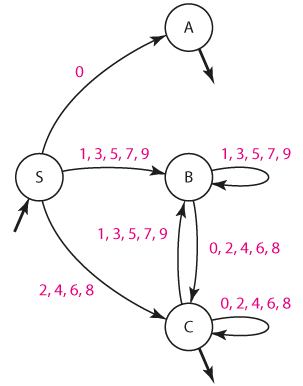
Gramatika je pak jednoduše:

S --> 0A
S --> 1B | 3B | 5B | 7B | 9B
S --> 2C | 4C | 6C | 8C
A --> e
B --> 1B | 3B | 5B | 7B | 9B
B --> 0C | 2C | 4C | 6C | 8C
C --> 0C | 2C | 4C | 6C | 8C
C --> 1B | 3B | 5B | 7B | 9B
C --> e

Aritmetické výrazy

Napište gramatiku, která bude generovat aritmetické výrazy odpovídající libovolně uzávorkovanému součtu libovolně mnoha identifikátorů. Identifikátor budeme značit písmenem i, množina terminálních symbolů tak bude T = { i, +, (, ) }. Příklady výrazů: i, i+i, i+(i+i+i).

Gramatiku můžeme odvodit díky jednoduché úvaze: aritmetický výraz je buď samotný identifikátor, nebo součet libovolných aritmetických výrazů, nebo libovolný aritmetický výraz v závorkách. Nahradíme-li slovní spojení "aritmetický výraz" neterminálním symbolem S, zapíšeme jednotlivé případy do gramatiky G takto:

G:   S --> i             (1)
     S --> S + S         (2)
     S --> (S)           (3)

Příklady aritmetických výrazů uvedených výše můžeme gramatikou snadno odvodit:

Postup odvozování můžeme přehledně znázornit tzv. derivačním stromem; práce s derivační stromy je pak jádrem činnosti překladače počítačového jazyka. Pro výraz  i + ( i + i + i )  vypadá takto; modře jsou zvýrazněny terminální symboly. Podotkněme, že výsledný výraz získáme, vypíšeme-li listy stromu průchodem in-order.

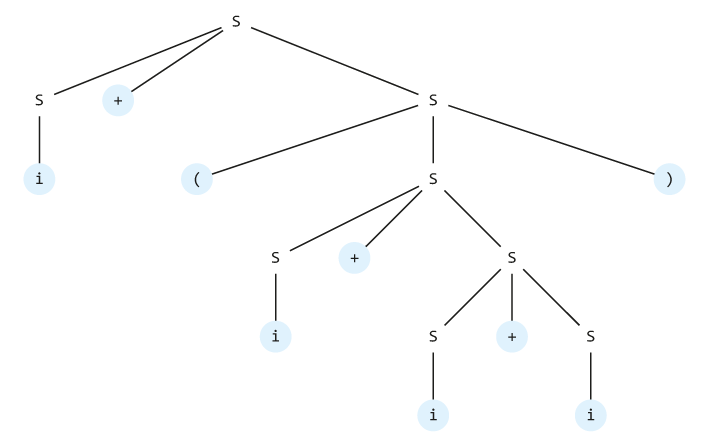
Všimněme si jak ve stromu, tak v přepisu pomocí pravidel gramatiky jisté nejednoznačnosti. U pátého řádku přepisování (červeně zvýrazněného) není zřejmé, zda se pravidlem 2 rozvinul první, nebo druhý neterminální symbol S. Derivační strom ukázal možnost, kdy byl přepsán druhý ze symbolů. Alternativně je tedy možné nakrelit jiný derivační strom, který vede ke stejnému výsledku; pozměněná část je čárkovaně zvýrazněna.

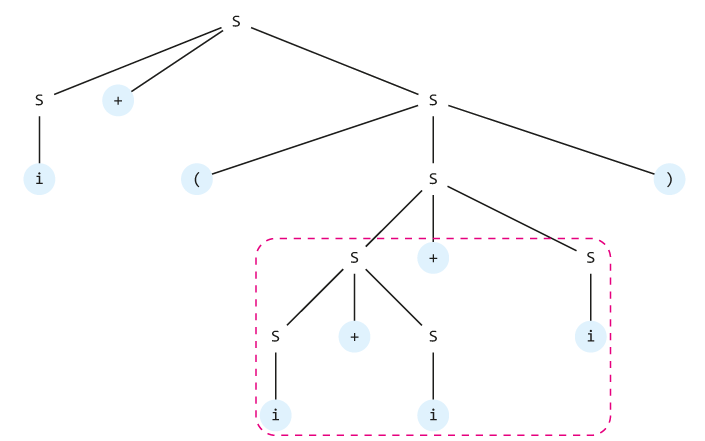
Gramatice, která nevede k jednoznačně určenému derivačnímu stromu, říkáme nejednoznačná. Zejména při konstrukci překladačů, kde gramatiky hrají významnou úlohu, se snažíme nejednoznačným gramatikám vyhýbat.

Naštěstí lze některé nejednoznačné gramatiky nahradit ekvivalentními jednoznačnými gramatikami. V našem případě vypadá ekvivalentní gramatika G' takto:

G':  S --> T                    (1)
     S --> S + T                (2)
     T --> i                    (3)
     T --> (S)                  (4)

Ekvivalenci gramatik symbolicky zapíšeme výrazem L(G) = L(G'), čili jazyky generované gramatikami G a G' jsou stejné.

Snadno se přesvědčíme, že gramatika G' rovněž dokáže generovat výraz  i + ( i + i + i ) , ale tentokrát bez nejednoznačnosti.

S --> S + T                     (2)
  --> T + T                     (1)
  --> i + T                     (3)
  --> i + ( S )                 (4)
  --> i + ( S + T )             (2)
  --> i + ( S + T + T )         (2)
  --> i + ( T + T + T )         (1)
  --> i + ( i + T + T )         (3)
  --> i + ( i + i + T )         (3)
  --> i + ( i + i + i )         (3)

Napište gramatiku, která bude generovat libovolně uzávorkované aritmetické výrazy s identifikátory i a operátory +, -, ×, /.

Jednoznačná gramatika, která vyhovuje zadání, vypadá například takto:

S --> T | S + T | S - T        (1a, 1b, 1c)
T --> F | T × F | T / F        (2a, 2b, 2c)
F --> i | (S)                  (3a, 3b)

Pravidla 1a až 1c říkají, že aritmetický výraz S se dá napsat jako sekvence několika neterminálních symbolů T (tzv. termů) oddělených operátory sčítání nebo odčítání. Pravidla 2a až 2c říkají, že term T se dá napsat jako sekvence několika neterminálních symbolů F (tzv. faktorů) oddělených operátory násobení nebo dělení. Konečně pravidla 3a a 3b říkají, že faktor F je buď jednoduchý identifikátor, nebo libovolný aritmetický výraz S v závorkách.

Již několikrát jsme poznamenali, že konstrukce derivačního stromu a manipulace s ním tvoří jádro činnosti překladače. Naznačme si to na příkladu výrazu "1 + 2 × 3", kde čísla 1, 2, 3 jsou hodnoty identifikátorů.

Derivační strom nakreslíme snadno:

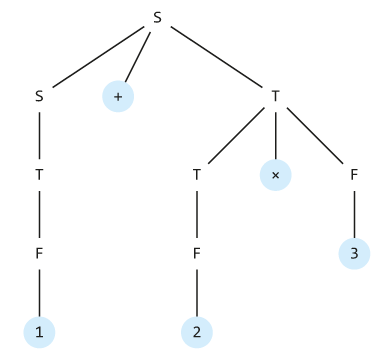
Nyní si uvědomme, jak vlastně může překladač vyhodnotit výsledek aritmetického výrazu.

Celý aritmetický výraz, a tedy i jeho hodnota, je dán kořenem stromu. Chceme-li znát hodnotu celého výrazu, musíme vyhodnotit jeho levý podstrom, pravý podstrom a výsledky sečíst. Celý proces tak můžeme zapsat rekurzivním průchodem stromem. V pseudokódu by vypadal asi takto:

int zjistiHodnotu(vrchol X) 
{
  if (X je listem) 
  {
    return X.hodnota;
  } 
  else if (X má jen jednoho následníka) 
  {
    return zjistiHodnotu(X.následník);
  } 
  else // X má tři následníky
  {
    int l, p;
    l = zjistiHodnotu(X.levýNásledník);
    p = zjistiHodnotu(X.pravýNásledník);
    switch (X.prostředníNásledník.hodnota) {
      case '+' : return l + p;
                 break;
      case '-' : return l - p;
                 break;
      case '×' : return l * p;
                 break;
      case '/' : return l / p;
                 break;
    }
  }
}

Hodnotu výrazu bychom snadno zjistili voláním

hodnotaVýrazu = zjistiHodnotu(kořenStromu);

A jak funguje překladač? Dejme tomu, že máme mikroprocesor, který dokáže hospodařit se zásobníkem. Má pět instrukcí:

Samotný překladač by měl generovat instrukce, které se uloží do spustitelného souboru (.exe). Překladač by vypadal asi takto:

void preloz(vrchol X) 
{
  if (X je listem) 
  {
    generujInstrukci(PUSH X.hodnota);
  } 
  else if (X má jen jednoho následníka) 
  {
    preloz(X.následník);
  } 
  else // X má tři následníky
  {
    preloz(X.levýNásledník);
    preloz(X.pravýNásledník);
    switch (X.prostředníNásledník.hodnota) {
      case '+' : generujInstrukci(ADD);
                 break;
      case '-' : generujInstrukci(SUB);
                 break;
      case '×' : generujInstrukci(MUL);
                 break;
      case '/' : generujInstrukci(DIV);
                 break;
    }
  }
}

Po zavolání

preloz(kořenStromu);

by překladač postupně vygeneroval instrukce

PUSH 1
PUSH 2
PUSH 3
MUL
ADD

Mikroprocesor, který by je měl tyto instrukce provést, by napřed uložil do zásobníku hodnoty 1, 2, 3. Obsah zásobníku by pak vypadal takto (vrchol je nahoře):

3
2
1

Pak by se dvěma čísly z vrcholu zásobníku (2, 3) provedl instrukci násobení a výsledek (6) by uložil zpět. Zásobník by nyní vypadal takto:

6
1

Na závěr by provedl instrukci sčítání a výsledek opět uložil zpět:

7

V zásobníku tedy zůstala vyčíslená hodnota aritmetického výrazu.

Samostatně si vyzkoušejte/promyslete:

Zpět na hlavní stránku

Poslední úprava 2016/9/15