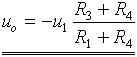Příklady výpočtů operačních sítí

Příklad č.1

Vypočítejte obecně výstupní napětí u_o v závislosti na vstupních napětích u₁ a u₂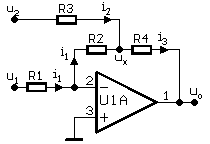

Řešení pomocí přímé aplikace Ohmova a Kirhoffových zákonů:

Vlivem záporné zpětné vazby je mezi vstupy OZ virtuální nula, do vstupů ideálního OZ proudy netečou, lze tedy snadno vypočítat hodnotu proudu i₁:

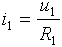
Dále lze pomocí vypočteného proudu i₁ určit napětí u_x:

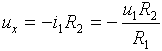
Nyní můžeme stanovit hodnotu proudu i₂:

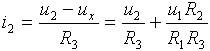
Proud i₃ protékající rezistorem R₄ je dán součtem proudů i₁ a i₂:

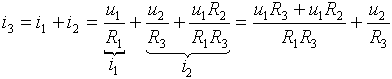
Hledané výstupní napětí je dáno součtem napětí u_x s úbytkem napětí na rezistoru R₄:

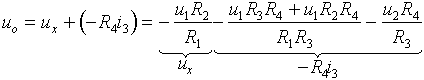
Po úpravě dostáváme konečný výsledek:

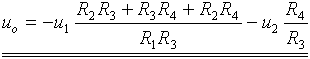
Řešení pomocí principu superpozice:

Výpočet rozdělíme na dvě části, nejprve provedeme výpočet u_o1 pro u₂ = 0, poté provedeme výpočet u_o2 pro u₁ = 0. Výsledné napětí u_o je dáno součtem dílčích výsledků u_o1 a u_o2.

Výpočet pro u₂ = 0:

Vlivem záporné zpětné vazby je mezi vstupy OZ virtuální nula, do vstupů ideálního OZ proudy netečou, lze tedy snadno vypočítat hodnotu proudu i₁:

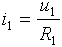
Dále lze pomocí vypočteného proudu i₁ určit napětí u_x:

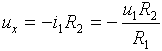
Nyní můžeme stanovit hodnotu proudu i₂:

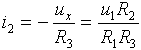
Proud i₃ protékající rezistorem R₄ je dán součtem proudů i₁ a i₂:

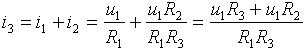
Hledané dílčí výstupní napětí u_o1 je dáno součtem napětí u_x s úbytkem napětí na rezistoru R₄:

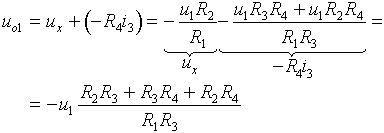
Výpočet pro u₁ = 0:

Vlivem záporné zpětné vazby je mezi vstupy OZ virtuální nula, do vstupů ideálního OZ proudy netečou, platí tedy:

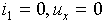
Vypočteme tedy hodnotu proudu i₂:

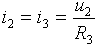
Dílčí výstupní napětí u_o2 je rovno úbytku napětí na rezistoru R₄:

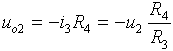
Výsledné napětí u_o je dáno součtem napětí u_o1 a u_o2:

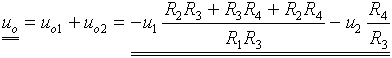
Jak je vidět, obě metody řešení vedou ke stejnému správnému výsledku, liší se pouze náročností a délkou výpočtu. V některých případech je výhodnější výpočet první metodou v jiných případech vyjde jednodušší výpočet druhou metodou. Je tedy na Vás, kterou z metod při výpočtu použijete.

Příklad č.2

Vypočítejte obecně výstupní napětí u_o v závislosti na vstupním napětí u₁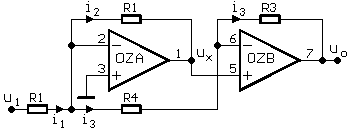

Ze schématu je zřejmé, že oba operační zesilovače mají zápornou zpětnou vazbu a lze tedy u nich uvažovat nulové napětí mezi vstupy (virtuální nulu). Neinvertující vstup OZA je uzemněný, na invertujícím vstupu je tedy také nulové napětí a lze tedy snadno vyjádřit proud i₁:

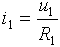
Tento proud se dělí na proudy i₂ a i₃. Vzhledem k tomu, že oba proudy tečou mezi stejnými potenciály (mezi vstupy OZB je nulové napětí), rozdělí se v opačném poměru odporů větví, kterými tečou (proudový dělič). Proud i₂ tekoucí rezistorem R₁ je tedy:

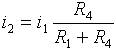
A proud i₃ tekoucí rezistorem R₄ je:

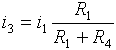
Nyní již lze vyjádřit napětí u_x na vstupech druhého operačního zesilovače OZB. Toto napětí je možno vyjádřit jako úbytek napětí na rezistoru R₁ způsobený proudem i₂ nebo jako úbytek napětí na rezistoru R₄ způsobený proudem i₃, obě varianty jsou ekvivalentní a platí tedy:

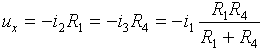
Po úpravě:

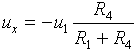
Hledané výstupní napětí je dáno součtem napětí u_x a záporně vzatého úbytku napětí na rezistoru R₃. Tento úbytek je:

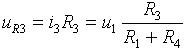
Výstupní napětí u_o je tedy:

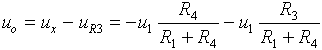
Po úpravě dostáváme výsledný tvar:

Příklady na výpočty operačních sítí